The problem of stability of the Solar System was enunciated by Isaac Newton after establishing his law of gravitation. If we consider a single planet around the Sun, we well retrieve the elliptical motion of Kepler. However, once several planets orbit around the Sun, they are subject to their mutual attraction, which disturbs their movement. Until recently, scientists have accepted a regular and quasi-periodic picture for the motion of the planets, allowing no collisions or close encounters. Just 20 years ago, using numerical computations, Jacques Laskar showed that the motion of the solar system is chaotic. Therefore, it is impossible to precisely predict the motion of the planets over more than a few tens of millions of years (Myr). It is then not sufficient to calculate a single orbit of the movement to answer the question of stability of the Solar System, i.e. whether a collision with another planet or the Sun is possible in less than 5 billion years (Gyr), before the end of the life of the Sun when it becomes a red giant. In 1994, Jacques Laskar, in a previous long-term study has shown that the chaotic diffusion of the orbit of Mercury is such that a close encounter or a collision with Venus is possible in less than 5 Gyr. To achieve this, he used averaged equations which allowed to divide the computing time by more than 1,000. However, this approximation is no longer valid in the vicinity of the collisions. A statistical study on a comprehensive and non averaged model, including the contributions of general relativity was therefore necessary. Such a study is described in the Nature issue of 11 June 2009. Thanks to the calculations already made, it appeared that it was necessary to make numerous simulations of the movement of the Solar System over 5 Gyr, because the estimated probability of collisional events was low. Thus, in order to achieve a significant statistical study, Jacques Laskar and Mickael Gastineau (IMCCE/Paris Observatory/UPMC/CNRS) calculated over 2500 trajectories of a realistic model of the Solar System, including general relativity and the contribution of the Moon.
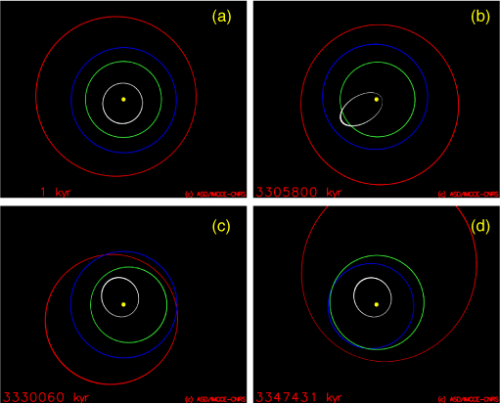
Each solution requiring nearly 4 months of computation, the researchers had to use computers from Paris Observatory, from the Institute of Earth Physics of Paris, and from the EGEE node of the Laboratory of the Linear Accelerator. Finally, it is the installation of the new JADE supercomputer at the National Computing Center CINES that allowed to find the 7 million hours of CPU time required to conclude this work. The 2500 calculated solutions are compatible with our best knowledge of the Solar system. In the majority of the cases, the planets continue to evolve as in the most recent few million years: the planetary orbits become deformed and precess under the planetary mutual perturbations, but without possibility of collisions or ejection out of Solar system. Nevertheless, in about 1% of the cases, Mercury’s eccentricity increases considerably. In several cases, this deformation of the orbit of Mercury leads to a collision with Venus or with the Sun in less than 5 Gyr while the orbit of the Earth remains little affected. In contrast, for one of these orbits, the increase of the eccentricity of Mercury is followed by an increase in the eccentricity of Mars, and a complete destabilization of the inner Solar System (Mercury, Venus, Earth, Mars) in 3.4 Gyr. Among 201 cases examined starting from this destabilization time, 5 examples led to the ejection of Mars out of the Solar System. All other cases lead to collisions between planets or between a planet and the Sun in less than 100 million years. One case resulted in a collision between Mercury and the Earth, 29 cases in a collision between Mars and Earth and 18 to a collision between Venus and the Earth.

CNRS press release Existence of collisional trajectories of Mercury, Mars and Venus with the Earth J. Laskar & M. Gastineau Nature 11/06/2009. Contact Jacques Laskar (Observatoire de Paris, IMCCE, & CNRS)
Last update on 21 December 2021