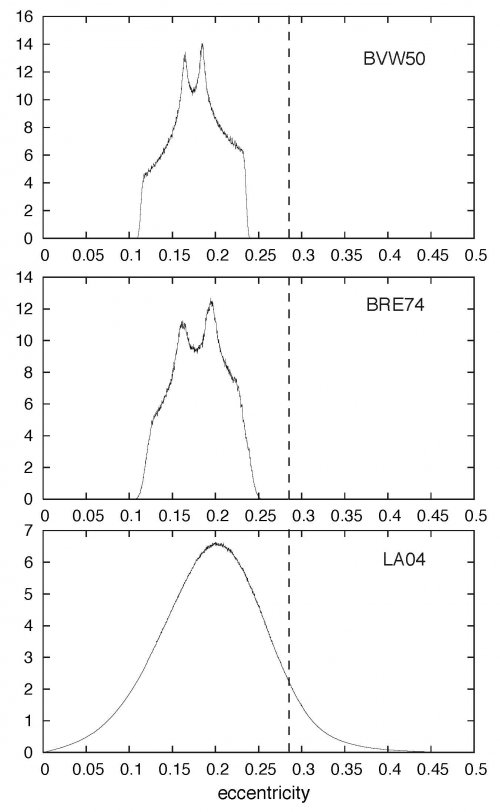
Indeed, the tidal dissipation due to the Sun will bring the rotation rate of Mercury towards a limit value that depends on the eccentricity of the planet. For an eccentricity close to zero, tidal dissipation drives the planet towards a synchronous state, where Mercury would rotate once every revolution around the Sun, like the Moon around the Earth. But if the eccentricity is not zero, the limit value is larger than 1 (with respect to the orbital motion). In particular, the resonant value 3/2 is obtained for the critical value e_3/2 = 0.285.As the motion of the Solar System is chaotic (Laskar, 1989, 1994), it is not possible to trace back the orbital motion of the planets over more than a few tens of millions of years. In order to study the distribution of Mercury’s eccentricity in the past 4 Gyr, Jacques Laskar and Alexandre Correia have computed 1000 different orbits of the whole Solar System, over 4 Gyr, starting with very close inititial conditions, using the computers of Paris Observatory and of the national computing centre of CNRS (IDRIS) for several months. The resulting density function for the eccentricity of Mercury is given in figure 2 (LA04). The main difference with respect to the previous solutions BVW50 and BRE74, is that the eccentricity of Mercury can increase beyond the critical value e_3/2, allowing for additional possibilities of capture into the 3/2 resonance. Click on the image to enlarge itContrarily to what was assumed before, the capture will not necessary occur at the first crossing of the resonance, during the initial spin down of the planet. As the eccentricity of Mercury is changing (because of the perturbations from the other planets in the Solar System), the limit value of the rotation rate will change, and cross again the 3/2 value, giving rise to additional possibilities of capture into resonance (Fig. 3). Even if the probability of capture at each crossing is small, the existence of multiple crossings will largely increase the total probability of capture into the 3/2 resonance.(a) is the classical case, for which the limit value of the rotation rate is always below the resonant value 1.5. (b) and (c) are new possibilities of capture resulting from the chaotic evolution of Mercury’s eccentricity. In (b), the eccentricity of Mercury is close to its critical value at the time of the initial spin down of the planet. Multiple crossings of the resonance occur and the probability of capture is largely enhanced. In (c), the planet rotation was not initially captured into resonance, but much later on, as the eccentricity of the planet increases, the rotation is accelerated and the planet can be captured again. Click on the image to enlarge itWith their extended numerical simulations, the researchers found that the capture into the 3/2 resonance is in fact the most probable outcome of the planet, with 55.4 % chances to occur. The remaining possibilities being a capture into the 1/1 resonance (2.2%) as for the Earth-Moon system, capture into the 2/1 resonance (3.6%), or no capture (38.8%). Temporary capture into higher order resonances (5/2 or 3/1 for example) are possible, but none of them survived over the full integration, as they become destabilized when the eccentricity of Mercury decreases to low values.The same research team have already shown three years ago (Correia and Laskar, 2001) that the retrograde rotation of Venus can be naturally explained by the consideration of the various involved dissipative effects and the existence of the large chaotic zone for the obliquity, resulting from the planetary perturbations (Laskar and Robutel, 1993).The four final rotation states of Venus, Alexandre C. M. Correia et Jacques Laskar, Nature, 411, 767—770, 14 June 2001 Large-scale chaos in the solar system, Jacques Laskar Astronomy and Astrophysics, 287, L9-L12, 1994 The chaotic obliquity of the planets, Jacques Laskar and Philippe Robutel, Nature, 361, 608-612, 18 February 1993 A numerical experiment on the chaotic behaviour of the Solar System, Jacques Laskar Nature, 338, 237-238, 16 Mars 1989
Last update on 21 December 2021